[백트래킹] 정의 및 활용 예시

🔎 백트래킹이란?

해를 찾는 도중 해가 아니어서 막히면 되돌아가서 다시 해를 찾아가는 기법

→ 지금의 경로가 해가 될 것 같지 않으면 그 경로를 더이상 가지 않고 되돌아간다 == 가지치기

(가지치기를 얼마나 잘하느냐에 따라 효율성이 결정된다!)

 

백트래킹 기법의 유망성 판단

어떤 값이(어떤 노드가) 해가 될 가능성이 있다면 유망하다고 하며, 유망하지 않은 값에 가지 않는 것을 가지치기라고 한다. 유망하지 않다고 판단되면 그 값의 이전으로 돌아가 다음 값으로 넘어간다. (이전 노드로 돌아가 다음 자식 노드로 간다.)

---

🔎 DFS vs 백트래킹 vs 분기한정법

DFS	가능한 모든 경로를 깊이 우선으로 탐색하는 것 (한 방향으로 갈 수 있는 경로를 먼저 탐색) → 현재 정점과 인접한 간선들을 모두 검사하여 아직 방문하지 않은 정점으로 향하는 간선이 있는 경우 해당 간선을 무조건 따라가는 것	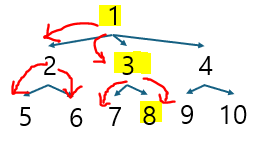'138'을 탐색할 때 두 번째 숫자가 원하는 값이 아님에도 불구하고 끝까지 탐색 진행
백트래킹	현재 가는 길이 더 이상의 해가 아니라고 판단되면 돌아옴	'138'을 탐색할 때 두 번째 숫자가 원하는 값이 아니면 탐색 종료, 다음으로 넘어감
분기한정법	최적해를 찾을 가능성이 없으면 분기하지 않음 → 많은 유망 노드 중 가장 좋은 유망 노드를 선택하여 결정 "최적의 해를 구하는 문제에 사용하기 위한 방법" - 유망하다 : 한계치가 이전까지 찾은 최적의 해답보다 더 좋다 - 유망하지 않다 : 한계치가 지금까지 찾은 최적의 해답보다 더 좋지 않다 - 가지치기 : 유망하지 않으면 더 이상 가지를 뻗어 탐색하지 않음 * 한계치 : 그 노드로부터 가지를 뻗어나가서 얻을 수 있는 해답의 한계	bfs, dfs, best-first-search를 사용해서 구현할 수 있지만 일반적으로 best-first-search로 구현한 것이 결과가 좋다 * best-first-search : 비용이 가장 적은 노드를 예측하여 가장 먼저 탐색하는 기법으로 너비 우선 탐색과 깊이 우선 탐색 알고리즘의 장점을 결합한 것 → priority queue 사용

 

참고

https://sojeong-lululala.tistory.com/184

[이진탐색] 깊이 우선 탐색[DFS]과 백트래킹[Backtracking] 차이점

 

---

📑 예제

✅ N과 M (1)

https://www.acmicpc.net/problem/15649

15649번: N과 M (1)

문제 설명

코드 예시

 

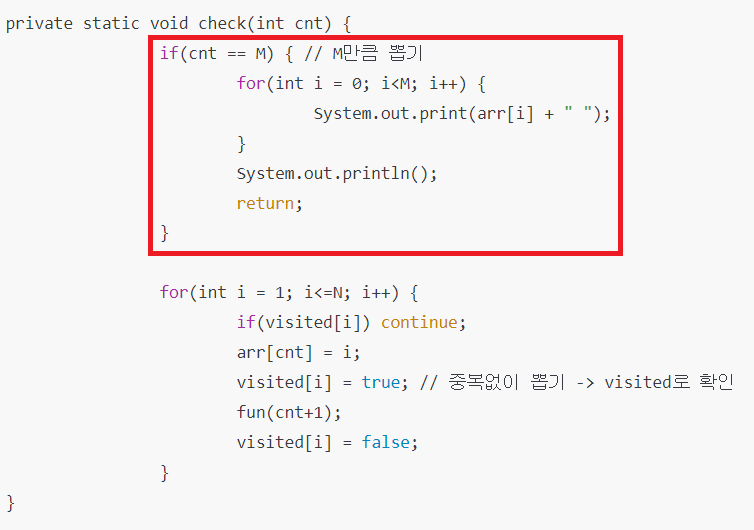
1. 탐색 과정에서 값을 담을 int 배열, 방문한 노드 체크를 위해 boolean 배열(visited) 생성

2. 재귀가 깊어질 때마다 cnt를 1씩 증가해서 M과 같아지면 더 이상 재귀 호출 X 

 

 

✅  N-Queen

https://www.acmicpc.net/problem/9663

9663번: N-Queen

 

문제 설명

＊퀸은 상하좌우, 대각선 4방향으로 거리 제한 없이 이동 가능 == 같은 행X, 같은 열X, 대각선X

 

코드 예시

 

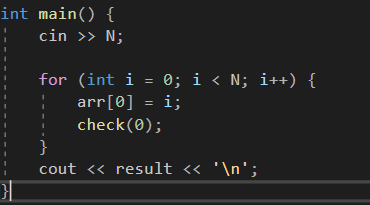
＊메인 함수에서 arr[0](0열)에 0~N-1까지 넣어서 각각 퀸 배치가 가능한 경우의 수를 탐색하도록 함

 

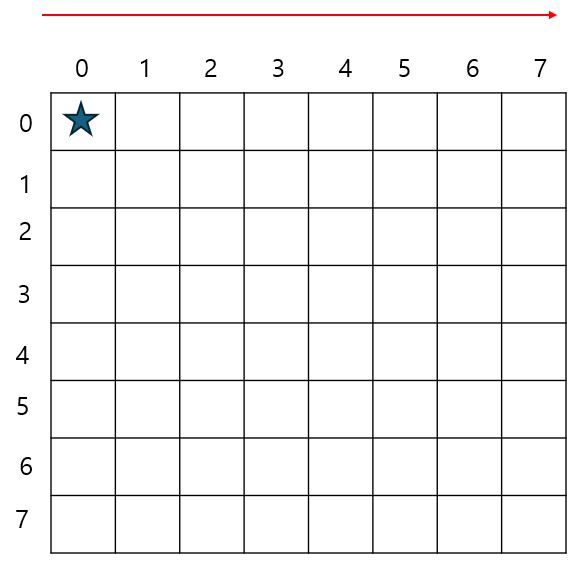
1. 첫번째 퀸을 (0,0)에 배치했을 때의 경우의 수 계산

 

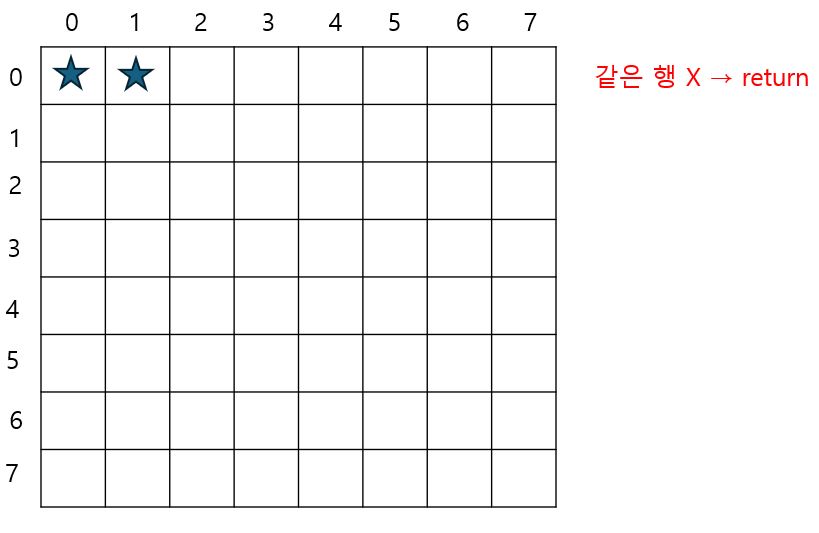
2. 두번째 퀸을 0부터 배치하여 이전에 배치한 퀸의 위치와 비교해서 조건에 부합하는지 확인

(위 그림의 경우, 퀸은 같은 행에 배치할 수 없기 때문에 return됨)

 

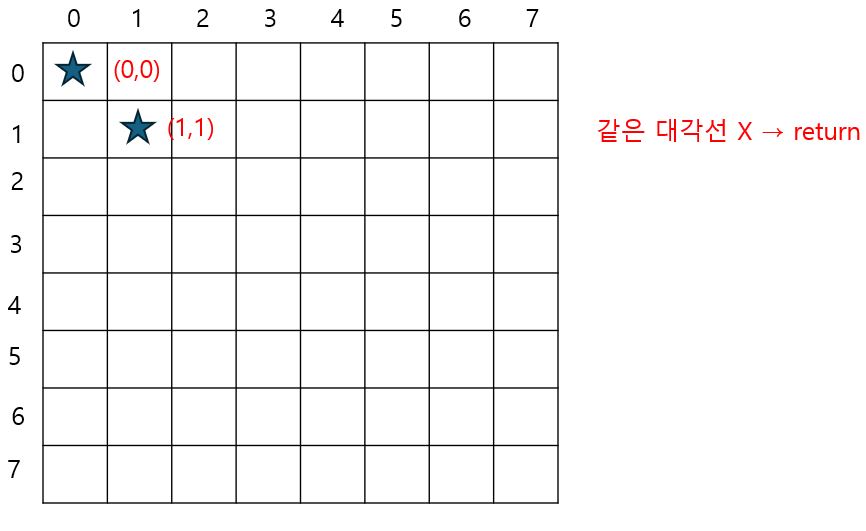
3. 첫 번째 행(인덱스 0)에 배치가 불가능하기 때문에 두 번째 행(인덱스 1)으로 옮기고( → check 함수의 두 번째 for문으로 표현) 다시 재귀를 통해 조건에 부합하는지 판별

(위 그림의 경우, 퀸은 같은 대각선에 배치할 수 없기 때문에 return됨)

 

 

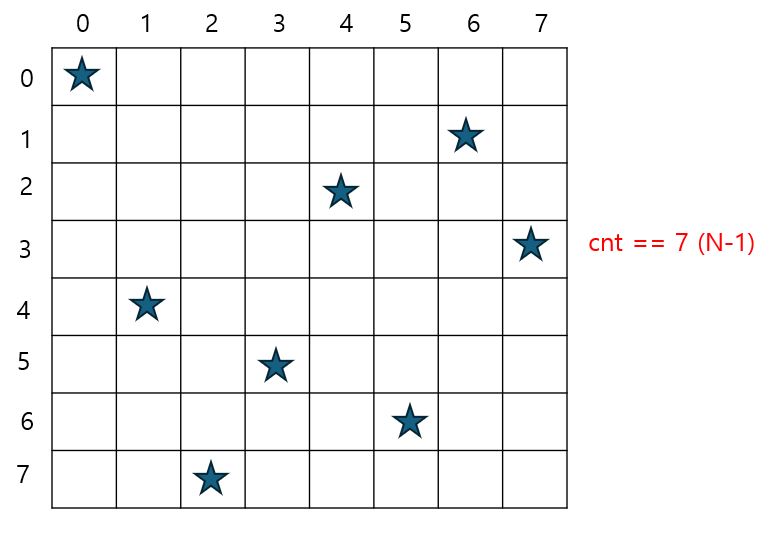
4. 1번부터 3번까지 반복해서 조건에 맞는 퀸 배치를 찾고 cnt가 N-1이 되는 순간 result(경우의 수)를 1 증가시켜준다

 

* 정리

 

1. 첫번째 열(인덱스 0)을 0~N-1행에 배치 

for(int i = 0; i<N; i++) { arr[0] = i; check(0); }

 

2. 현재 퀸의 위치가 조건에 부합하는지 판별

for(int i = 0; i<cnt; i++) 
	if(arr[i] == arr[cnt] || abs(i-cnt) == abs(arr[i] - arr[cnt])) return;

 

2-1. 조건 X → 함수를 종료하고 호출한 곳으로 돌아가 퀸의 위치를 다음 행으로 옮겨줌

2-2. 조건 O → 다음 퀸의 위치 판별 

for(int i = 0; i<N; i++) {
	arr[cnt + 1] = i;
    check(cnt + 1);
}

 

3. N-1개의 퀸 배치가 끝나면 result 증가

if(cnt == N - 1) {
	result++; 
	return;
}

 

 

 

✅  부분 수열의 합

https://www.acmicpc.net/problem/1182

1182번: 부분수열의 합

 

💻 코드

#include <iostream>
using namespace std;

int N, S;
int arr[21];
int selected[21];
int result = 0;

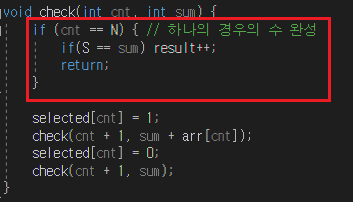
void check(int cnt, int sum) {
	if (cnt == N) { // 하나의 경우의 수 완성
		if(S == sum) result++; 
		return;
	}
	
	selected[cnt] = 1;
	check(cnt + 1, sum + arr[cnt]);
	selected[cnt] = 0;
	check(cnt + 1, sum);
}

int main() {
	cin >> N >> S;

	for (int i = 0; i < N; i++) {
		cin >> arr[i];
	}

	check(0, 0);
	if (S == 0) cout << result - 1 << '\n';
	else cout << result << '\n';
}

 

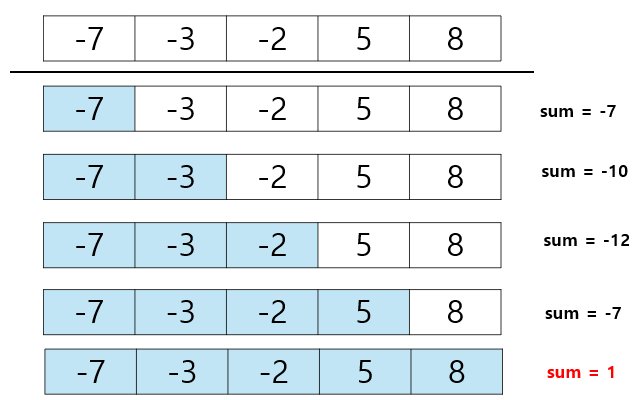
* 부분 집합 활용

 

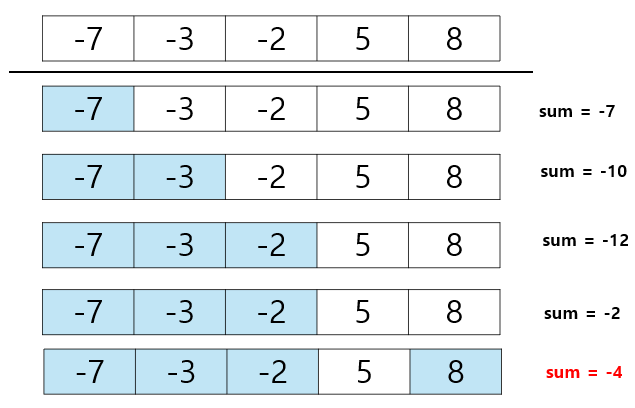
① 원소 5개 모두 선택 : {-7, -3. -2, 5, 8}

 

② 원소 4개 선택 (1) : {-7, -3, -2, 5}

 

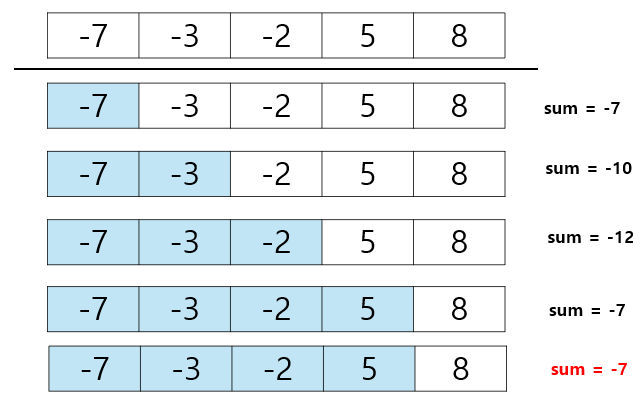
③ 원소 4개 선택 (2) : {-7, -3, -2, 8}

 

 

✅  암호 만들기

https://www.acmicpc.net/problem/1759

1759번: 암호 만들기

 

 

💻 코드

#include <iostream>
#include <algorithm>
using namespace std;

int L, C;
char arr[101];
int selected[101];

void check(int cnt, int start) {
	if (cnt == L) {
		int con = 0, vo = 0;
		string pass = "";
		for (int i = 0; i < L; i++) pass += arr[selected[i]];

		for (int i = 0; i < pass.length(); i++) {
			if (pass[i] == 'a' || pass[i] == 'e' || pass[i] == 'i' || pass[i] == 'o' || pass[i] == 'u') vo++;
			else con++;
		}

		if (vo >= 1 && con >= 2) cout << pass << '\n';
		return;
	}

	for (int i = start; i < C; i++) { // 문자가 저장된 각 인덱스를 선택
		selected[cnt] = i;
		check(cnt + 1, i + 1); 
	}
}

int main() {
	cin >> L >> C;
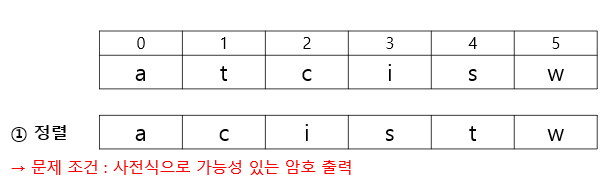
	for (int i = 0; i < C; i++) cin >> arr[i];
	sort(arr, arr + C);
	check(0, 0);
	return 0;
}

 

* 조합

 

① C개의 문자를 입력 받고 정렬

 

② 서로 다른 L개의 문자를 선택해서 암호 만들기

string pass = "";
for (int i = 0; i < L; i++) pass += arr[selected[i]];

 

선택된 인덱스에 위치한 문자를 가져와서 string 문자열 생성

→ pass : acti

 

③ 암호 조건에 부합하는지 판별

→ 최소 한 개의 모음과 최소 두 개의 자음으로 구성

for (int i = 0; i < pass.length(); i++) {
	if (pass[i] == 'a' || pass[i] == 'e' || pass[i] == 'i' || pass[i] == 'o' || pass[i] == 'u') vo++;
	else con++;
}

if (vo >= 1 && con >= 2) cout << pass << '\n'; // 가능성 있는 암호 출력

 

④ 2번 3번을 반복하여 입력받은 C개의 문자로 만들 수 있는 모든 조합에 대해 암호 가능성 판별